Valorisation intégrale d'eau de pluie
Qualité d'eau de pluieEau à usage non alimentaireEau biocompatible
Les eaux hydrogénées
Sur la notion du rH2
Échanges de charges électriques dans l’eauLa première ambiguïté de la notion de l'ORPLa signification profonde de la notion du rH2La deuxième ambiguïté de l'ORPLa quantification W de Vincent
Chlore et irradiation UVMise en place de PLUVALOREntretien et utilisation de citerneSystèmes de filtrationSystème PLUVALOR dans le commercesur le site eautarcie.org
Texte de Joseph Országh.
La compréhension de ce chapitre demande des connaissances de base en chimie générale, niveau baccalauréat ou au mieux niveau première année du graduat en sciences. Elle permet de comprendre non seulement la portée réelle des différents procédés d'électrolyse de l'eau, mais également la notion de l'eau biocompatible. Cependant, ceux qui n'ont pas ces bases scientifiques peuvent également parcourir le texte et, même sans les formules chimiques et mathématiques, comprendre dans les grandes lignes l'idée de base.
La notion du rH2 n'est malheureusement pas enseignée dans les écoles, ni dans la plupart des facultés universitaires. Pourtant, l'ignorance de cette notion, lors de la perception et l'évaluation des phénomènes liés aux réactions de transferts d'électrons e- et de protons H+ , peut induire en erreur même les spécialistes.
Dans le domaine de la santé, cette notion-clef permet de comprendre et d'expliquer l'apparition d'un certain nombre de maladies graves et de tracer de nouvelles pistes de recherches pour le traitement de ces maladies. Il ne faut pas oublier que pratiquement toutes les réactions chimiques qui font fonctionner les êtres vivants sont des réactions de transferts de protons (acide-base) et de transferts d'électrons (redox). La théorie unitaire de ces deux types de réactions donne une idée juste des interdépendances intimes qui existent entre ces deux catégories de réactions. Ces interdépendances font comprendre les erreurs commises lorsqu'on ne tient compte que des réactions acide-base (la notion du pH) pour expliquer certaines anomalies de la santé (comme « l'acidification de l'organisme », sans tenir compte des réactions redox.
Ce texte est le résumé succinct de deux communications scientifiques de József Országh parues dans la revue Sciences du vivant (Éditions Arys, Paris):
Réactions oxydo-réduction et acido-basiques: Vers une approche théorique et expérimentale plus cohérente. Volume 1, pages 23-34 (1990)
L'eau en tant que système redox. Volume 2, pages 81-97 (1991)
La date de la première publication de ce texte sur le site www.eautarcie.org: 2011-03-01
Mise à jour: 2019-09-30
Théorie unitaire des réactions redox et acide-base – la signification de l’ORP
Échanges de charges électriques dans l’eau
Si l'eau et le milieu aqueux sont considérés comme un « miracle de la nature », c'est grâce à leurs propriétés remarquables liées aux échanges de charges électriques positives H+ ou protons et négatives e- ou électrons. Les premières constituent les réactions acide-base, les secondes celles d’oxydation-réduction. Dans tous les traités de chimie, ces deux catégories de réactions sont traitées dans deux chapitres séparés. Pourtant, s'agissant tout simplement de transferts de charges électriques, ces deux types de réactions peuvent, et doivent être décrits à l’aide d’un seul formalisme mathématique, la théorie unitaire des réactions de transferts de charges en milieu aqueux publiée en 1990 et en 1991. Comme nous allons le montrer, cette théorie met bien en évidence les liens intimes entre ces deux catégories de réactions. Les considérations développées ici ne sont évidemment valables qu'en milieu aqueux [1].
[1]
Remarque générale : Contrairement à certaines idées reçues, la dissolution des choses dans l'eau n'est pas un simple mélange entre les molécules d'eau et celles des substances qu'on y dissout. Dans l'écrasante majorité de cas, la dissolution s'accompagne d'une modification profonde des substances dissoutes. En dissolvant par exemple du sel de cuisine – du chlorure de sodium, NaCl – dans l'eau, il y a ce que les chimistes appellent dissociation électrolytique, suivant une véritable réaction chimique: NaCl(solide) → Na+(dissous) + Cl-(dissous). Les substances qui se dissocient en ions (comme l'ion de sodium Na+ ou l'ion chlorure Cl-) dans l'eau sont des électrolytes. Donc dans une soupe, en réalité, il n'y a plus de sel (chlorure de sodium), mais des ions Na+ et Cl-. Les ions portant une charge électrique positive sont des cations attirés par une électrode métallique appelé cathode portant des charges électriques négatives. De même, les ions portant une charge électrique négative sont des anions attirés par l'anode portant des charges positives.
La particularité principale de l'eau par rapport aux autres solvants est le fait qu'elle participe activement dans les réactions qui ont lieu en solution. L'eau se comporte comme base vis-à-vis des acides qu'on y introduit, et elle présente un caractère acide vis-à-vis des bases dissoutes. De même, vis-à-vis des réducteurs (donneurs d'électrons), elle se comporte en oxydant, tandis que vis-à-vis d'un oxydant (capteurs d'électrons), l'eau présente un caractère réducteur. Par ailleurs, comme nous allons montrer, une réaction entre un acide (donneur de protons) et une base (capteur de protons) ne se fait pas directement, mais par l'intermédiaire de l'eau. Celle-ci captera le proton H+ de l'acide et une autre molécule d'eau, située plus loin, cédera un autre proton à la base. C'est ainsi qu'une réaction de neutralisation acide-base a lieu dans l'eau. De même, la dissolution d'un réducteur (donneur d'électrons, comme la vitamine C) cédera à l'eau des électrons e-. Un oxydant (capteur d'électrons) présent recevra un autre électron, d'une autre molécule d'eau. C'est la réaction d'oxydoréduction qui n'est autre qu'une sorte de neutralisation. Donc la dissolution d'un oxydant, d'un réducteur, d'un acide ou d'une base modifie profondément les propriétés chimiques de l'eau – et par voie de conséquences – ses propriétés biologiques aussi. Une eau contenant des réducteurs (donneurs d'électrons) sera donc en quelque sorte « enrichie » d'électrons. Dans ce cas, nous disons de cette eau qu'elle est antioxydante.
Autoprotolyse de l'eau
Entre deux molécules d'eau, il peut y avoir un transfert spontané de proton (le proton est le noyau d'un atome d'hydrogène que l'on désigne par H+), une charge électrique positive, par une réaction d’« autoprotolyse »:
H3O+ + OH-Afin de simplifier l'écriture, les chimistes adoptent souvent une convention qui consiste à remplacer l'écriture de l'ion hydroxonium H3O+ (en fait du proton hydrolysé, à ne pas confondre avec l'ion « hydranion » H3O-) par un proton H+, sachant bien entendu qu'il s'agit seulement d'une convention d'écriture. En réalité, un proton ne peut jamais « se promener » seul dans l'eau sans être lié à une molécule de H2O, pas plus que l'hydranion. Dès lors, la réaction (1) s'écrit simplement:
H+ + OH-L'ion OH- est appelé hydroxyde. La constante d'équilibre Kw de la réaction (1a) d'autoprotolyse s'écrit:
...où [H+] et [OH-] sont les activités des protons et celles des ions d'hydroxydes. En première approximation [H+] et [OH-] peuvent souvent être assimilés à des concentrations molaires exprimées en mole/litre. En électrochimie et en thermodynamique, il est plus juste de parler d'activité au lieu de concentration. L'activité est un nombre sans dimensions.
Les acides, une fois dissous dans l'eau, libèrent de protons qui augmentent de ce fait l'activité des ions H+ (que nous désignerons par la suite par [H+] appelée activité protonique. Les bases, par contre, sont susceptibles de libérer des ions d'hydroxydes OH- en augmentant leur activité [OH-]. Cependant, en vertu de l'équation (2) en milieu aqueux, il s'établit toujours un équilibre entre ces deux ions, de manière à ce que le produit de leurs activités reste constant à une valeur de 10-14. Il y a donc une certaine « balance » entre les deux: lorsque l'activité des protons augmente, celle des ions hydroxydes diminue et inversement.
Pour caractériser l'acidité ou la basicité d'une solution aqueuse, un médecin et biochimiste danois, Sørensen, a introduit en 1909 la notion du « potentiel d'hydrogène » qu'il a désigné par pH2 [2], notion qui est devenue par la suite « pH », que l'on définit actuellement de la manière suivante: pH = -log[H+]. Parallèlement, on introduit aussi la notion complémentaire au pH, le pOH, défini d'une manière analogue: pOH = -log[OH-]. De même, la constante d'autoprotolyse peut également être exprimée sous la même forme logarithmique: pKw = -logKw = -log10-14 = 14. Dès lors, l'équation (2) peut être écrite sous une forme logarithmique:
L'état de référence des solutions aqueuses est évidemment l'eau chimiquement pure dans laquelle l'acidité et la basicité sont en équilibre: le milieu est dit neutre. Dans ce cas, les activités des protons et des ions hydroxydes sont identiques: [H+] = [OH-] = 10-7. Il en résulte que dans une solution où cette condition est remplie pH=-log10-7 = 7. C'est le point de neutralité acide-base. Les solutions dont le pH est situé entre 0 et 7 sont dites « acides », celles dont le pH se trouve entre 7 et 14 sont appelées « basiques » [2].
[2]
Sans le vouloir, avec son pH2, Sørensen a préfiguré la notion du rH2, complémentaire au pH, lancée en 1920 par le physico-chimiste américain W.M. Clark. En fait les deux grandeurs sont intimement liées à l'élément hydrogène dont la molécule est H2. Au contact de l'eau, cette molécule subit une véritable dissociation électrolytique : H2 + 2H2O H3O+] + H3O-] que l'on détecte par mesure du potentiel de la solution dans laquelle on fait barboter de l'hydrogène gazeux. Le pH de Sørensen n'est autre que -log[H3O+]], tandis que le rH2 de Clark est -log[H3O-]]. Le parallélisme entre les deux notions est plus qu'évident. Par ailleurs ni Sørensen, ni Clark (le créateur du rH2) n'étaient des électro-chimistes. Seulement, Sørensen avait plus de chance d'avoir des amis parmi les électro-chimistes de son époque que Clark qui, pour sa notion du rH2, a fait l'objet d'un véritable procès d'inquisition scientifique au sein de l'American Chemical Society. En 1924, il a été contraint de faire une autocritique en public et il a dû retirer son invention des places publiques. À cause de cela, la science de l'électrochimie a été privée d'un outil indispensable dont les conséquences commencent à devenir extrêmement gênantes et constituent une entrave devant le développement des applications prometteuses de l'électrochimie et de la thermodynamique, notamment en médecine.
Les solutions dont le pH est inférieur à zéro (donc avec un pH négatif) sont appelées « super acides ». Dans ces solutions l'activité des protons est supérieure à un. Les solutions avec un pH supérieur à 14, dans lesquelles l'activité des ions hydroxydes est supérieure à un sont des solutions « super basiques ». En biologie et en médecine, on ne rencontre pas de tels milieux aqueux.
Autoélectrolyse de l'eau
Les notions exposées dans le paragraphe précédent sont, en principe, connues des élèves de l'enseignement secondaire. Celles qui suivent sont nettement moins connues du public, même par les spécialistes.
En thermodynamique et en électrochimie des solutions aqueuses, l'état de référence est l'eau chimiquement pure. La réaction standard de formation de l'eau
H2O...est la base pour calculer les fonctions thermodynamiques de la molécule d'eau au départ des données calorimétriques et électrochimiques. L'inverse de cette réaction n'est autre que l'autoélectrolyse de l'eau qui a lieu lorsque 4 électrons e- (charges électriques négatives) sont échangés entre deux molécules d'eau, pour donner naissance à deux molécules d'hydrogène et à une molécule d'oxygène:
2 H2 + O2Pour rappel: l'autoprotolyse a lieu par échange d'un proton (charge électrique positive) entre deux molécules d'eau. Le parallélisme entre l'autoprotolyse et l'autoélectrolyse est évident. À ce sujet, voir le tableau. La constante d'équilibre Ke de la réaction (5) s'écrit donc:
En fait, l'oxygène de la molécule d'eau cède deux électrons aux deux atomes d'hydrogène. Ces deux atomes s'associent pour faire une molécule de dihydrogène H2. L'oxygène ayant perdu ses deux électrons en « cherche » un autre, étant dans le même cas, pour former la molécule de dioxygène O2 [3]. La constante d’autoélectrolyse de l’eau Ke peut être calculée au départ de l'enthalpie libre standard de la formation de l'eau.
[3]
Cette réaction est tout à fait marginale dans l'eau à un point tel qu'en moyenne une seule molécule de dihydrogène se forme dans 20 000 litres d'eau. C'est ce qui a incité les chimistes à dire que l'activité d'hydrogène [H2] dans l'eau « n'a pas de signification physique » puisqu'il n'y a pas d'hydrogène dans l'eau. Ils ont également argumenté sur la valeur extrêmement faible de la constante d'équilibre d'autoélectrolyse Ke. En appliquant le même raisonnement, il aurait fallu « jeter » une bonne partie des tables donnant les produits de solubilité de sels très peu solubles. Par exemple, le produit de solubilité du sulfure de mercure (HgS) est 10-53, celui du séléniure de mercure (HgSe) est 10-59. Il est évident que dans une solution « saturée » en ces sels, il n'y a ni ions de mercure ni ions de sulfure ou de séléniure. Les valeurs de produits de solubilité ont été calculées au départ des potentiels redox (ORP) mesurés dans ces solutions. On procède exactement de la même manière pour calculer le rH2 d'une solution aqueuse.
En dissolvant un réducteur dans l'eau, celui-ci aura tendance à céder des électrons à l'eau. Les oxydants, par contre, vont en capter. La présence d'un réducteur déplacera donc l'équilibre de l'autoélectrolyse vers la formation de l'hydrogène H2, tandis que les oxydants vont favoriser la tendance à l'apparition de l'oxygène O2. Ici aussi, grâce à l'équilibre (5), il y a balance entre les activités d'hydrogène [H2] et oxygène [O2]. Les deux activités changent en sens inverse, comme dans le cas de [H+] et [OH-].
La définition du rH2
À l'instar du pH pour les réactions acide-base, en 1920 (donc sept ans après l'introduction de la notion du pH), W.M. Clark [4] a défini la notion du rH2:
Accessoirement, nous pouvons aussi définir le rO2 = - log[O2]. Dès lors, compte tenu de l'équation (6), l'équation (3) pour les réactions redox prendra la forme
(#eq8)
[4]
En 1920, Clark a appelé cette notion « rH ». Le symbole rH2 – qui reflète mieux la réalité – n'est apparu que dans les années 1940. Clark a encore défini le rH comme étant « le logarithme négatif de la pression d'hydrogène dans l'eau »: rH = - logPH2. A l'époque, la notion d'activité thermodynamique n'était pas encore connue. L’erreur de Clark a été d’affirmer que « le rH est la mesure de la force oxydante ou réductrice d'une substance dissoute dans l'eau », ce qui est évidemment faux. Les contemporains de Clark n'ont pas compris le contenu génial de cette invention qui n'était en fait que le complément (indispensable) du pH de Sørensen. Suite à des discussions passionnées au sein de l'American Chemical Society, Clark a fini par céder à la pression de ses collègues. En 1924, il a reconnu son « erreur » et a conseillé à ses contemporains d'abandonner l'usage du rH. En dépit de cette autocritique, vu son caractère pratique, l'usage du rH s'est répandu dans les laboratoires du monde entier. Il a fallu attendre jusqu'à 1954 pour mettre de côté cette notion fondamentale. Source: W.M. Clark, « The Determination of Hydrogen Ions », Vol.2, Plenum New York (1920). Lire aussi l'article sur la mémoire de l'eau.
La « neutralité redox » ou la notion « d'indifférence redox »
Pour les réactions redox aussi, le milieu de référence est l'eau chimiquement pure dans laquelle les activités d'hydrogène [H2] et d'oxygène [O2] se répartissent dans les proportions de un oxygène pour deux hydrogène: [H2] = 2 [O2]. Calculons donc le rH2 de l'eau chimiquement pure. Pour cela, dans l'équation (6), remplaçons [O2] par ½[H2]:
...d'où l'on tire l'activité d'hydrogène dans l'eau pure: [H2] = 10-27,7 que les chimistes arrondissent à 10-28. Le rH2 de l'eau pure est donc -log10-28 = 28. C'est ce qu'on appelle le point de « neutralité redox » ou « indifférence redox ».
Donc, indépendamment de la valeur de son pH, une solution aqueuse n'est ni oxydante, ni réductrice (antioxydante) lorsque son rH2 est égal à 28. Une solution dont le rH2 est situé entre 0 et 28 est dite réductrice ou antioxydante. Lorsque la valeur du rH2 est comprise entre 28 et 42, la solution est dite oxydante [5].
[5]
En biologie, un milieu aqueux dont le rH2 est en dessous de 28, est appelé « anaérobie ». En effet, dans un tel milieu, l'activité d'oxygène [O2] est très faible. Les bactéries qui peuvent s'y développer ont une action chimiquement réductrice. Un exemple typique est la présence d'une culture d'azobacter susceptible de réduire en milieu anaérobie les ions nitrate NO3- en azote atmosphérique N2. En épuration des eaux, on appelle cela « dénitrification anaérobie ».
Dès que le rH2 monte au-dessus de 28, nous sommes en « aérobiose ». L'activité d'oxygène y étant plus élevée, ce sont d'autres types de bactéries qui s'y développent. En fait, chaque espèce de bactérie, virus ou de champignon microscopique a un domaine bien défini de pH et de rH2 dans lequel il peut se développer. En-dehors de leur domaine de pH et de rH2, ces êtres microscopiques meurent. Dans un système de coordonnées cartésiennes, on peut porter les valeurs du rH2 en fonction du pH pour obtenir un espace à deux dimensions, dans lequel le domaine d'existence de chaque bactérie ou de virus peut être délimité. On obtient ainsi une carte d'activité virale et bactérienne où chaque espèce occupe une place bien définie. Un tel diagramme est appelé « diagramme de Vincent
».
On peut à présent comprendre qu'une modification même modeste du rH2 du sang aura une influence décisive sur la possibilité de développement ou de disparition d’une bactérie ou d’un virus donné. Les applications médicales de l'électrochimie ouvrent ici des horizons prometteurs. L'usage de l'eau hydrogénée n'en est qu'un exemple. En fait, la valeur du rH2 du sang a aussi une influence décisive sur les potentiels électriques qui s'établissent à l'intérieur des cellules entre le noyau et le cytoplasme, ainsi qu'entre le cytoplasme et les liquides intercellulaires. Ces potentiels régulent aussi la division cellulaire, donc la genèse potentielle des cellules cancéreuses.
Les limites de stabilité des solutions aqueuses
Une solution dans laquelle l'activité d'oxygène [O2] = 1, rO2 étant zéro, en vertu de l'équation (8), le rH2 = 42. C'est la limite supérieure de stabilité thermodynamique d'une solution aqueuse. A cette valeur, il y a dégagement d'oxygène O2 gazeux et surtout formation d'oxygène atomique très réactif O: que les anciens appelaient « oxygène naissant ».
Une solution dans laquelle le rH2 est zéro a une 'activité d'hydrogène [H2] = 1. C'est la limite inférieure de stabilité thermodynamique d'une solution aqueuse. A cette valeur, l'eau se décompose et libère de l'hydrogène « naissant » H• électriquement neutre. Cet hydrogène a une affinité très grande vis-à-vis des radicaux libres, porteurs – eux aussi – d'un électron non apparié.
Une valeur négative pour le rH2 n'a, en principe, pas de signification physique. On a cependant mesuré dans des conditions particulières des valeurs négatives. Nous entrons ici dans le domaine de la thermodynamique des phénomènes irréversibles. Il s'agit là des solutions aqueuses instables au point de vue thermodynamique dans laquelle l'hydrogène naissant est temporairement stabilisé dans une autre formation moléculaire: l'hydranion H3O-. C'est probablement le cas des eaux hydrogénées.
La première ambiguïté de la notion de l'ORP
Le potentiel redox ORP est une mesure expérimentale (exprimée en volts ou en millivolts) largement utilisée pour caractériser les propriétés redox des solutions aqueuses. Il est généralement admis que plus l’ORP est élevé plus la solution est « oxydante »; plus il est bas plus la solution est réductrice ou « antioxydante ».
L'ORP lu sur un instrument de mesure possède deux ambiguïtés:
- Il n'est pas l'ORP réel qu'on utilise dans les calculs en électrochimie et en thermodynamique. Pour cela, la valeur lue doit être corrigée.
- Même l'ORP réel (donc corrigé) n'est qu'un des éléments pour se prononcer sur le caractère oxydant ou antioxydant d'une solution aqueuse.
Regardons à présent la première ambiguïté.
L'échelle conventionnelle des potentiels ORP
Examinons à présent la nature de l'ORP au point de vue électrochimique. Le point zéro de l'échelle des potentiels redox (ORP) n'est pas le potentiel zéro lu sur l'instrument de mesure. Ce potentiel ne représente nullement le point d'indifférence (ou neutralité) redox d'une solution, au-dessus duquel la solution est oxydante et en en dessous réductrice. En réalité, le potentiel zéro découle de la notion de limite de stabilité thermodynamique des solutions aqueuses. On réalise cette condition, dans l'électrode normale d'hydrogène. Il s'agit d'une électrode de platine métallique recouverte d'une mousse de platine, plongée dans une solution à pH = 0, dans laquelle on fait barboter de l'hydrogène gazeux H2 sous une pression de un bar.
L'hydrogène adsorbé dans les pores de la mousse de platine se comporte comme un élément à l'état condensé dont l'activité thermodynamique est égale à un: [H2] = 1. Donc le rH2 de l'électrolyte en contact avec l'électrode de platine est zéro. À pH = rH2 = 0, sur l'électrode de platine, on mesure un potentiel remarquablement stable dont la valeur est, en vertu de la loi de Nernst {équation (11)} zéro volt [6]. Le potentiel zéro thermodynamique possède donc une signification physique précise, sa valeur est liée à l'annulation simultanée du pH et du rH2.
[6]
Dans les traités actuels d'électrochimie, à propos de l'électrode normale d'hydrogène, on ne mentionne que la condition pH = 0. La condition de « pression d'hydrogène 1 bar ou 1atm » d'où [H2]=1, prête à confusion. En effet, sous cette pression la solubilité d'hydrogène dans l'eau n'est que de l'ordre du millième de mole/litre. Dans ce domaine de concentration, la teneur en hydrogène dissous peut, en première approximation, être assimilée à l'activité: [H2]. En liant le potentiel mesuré à la condition de pression d'hydrogène 1 bar, on fait une faute conceptuelle. Le rH2 de l'électrolyte en contact avec l'hydrogène et avec l’électrode de platine n'est en réalité pas zéro, mais environ 3.
Cette affirmation est facile à vérifier expérimentalement. En remplaçant l'électrode de platine platiné (mousse de platine) par une électrode brillante de platine, même sous une pression d'hydrogène de 1 bar et pH = 0, le potentiel mesuré se stabilise entre +85 et +90 millivolts au lieu de 0 millivolt. La raison est que le rH2 dans l'électrode brillante de platine, en dépit de la pression d'hydrogène de 1 bar, n'est pas zéro, mais environ –log10-3=3. Pour ramener le rH2 à zéro, l'hydrogène en contact avec le platine métallique doit être à l'état condensé: seul cet état peut avoir une activité thermodynamique égale à un. L'hydrogène gazeux « se condense » dans les cavités de la mousse de platine réduisant le rH2 à zéro. Il est donc plus simple et surtout plus cohérent de définir l'électrode normale d'hydrogène comme étant une électrode de platine dans laquelle le pH = rH2 = 0.
Afin de dissiper des malentendus conduisant à des erreurs, il convient de préciser que le potentiel ORP zéro lu sur un instrument, n'est pas l'ORP thermodynamique et ne correspond nullement au point d'indifférence redox au-dessus duquel on est en milieu oxydant et en dessous, en milieu réducteur ou antioxydant.
La mesure de l’ORP
Pour mesurer l'ORP d'une solution, on y plonge une électrode de platine (inerte vis-à-vis de l'eau) et une électrode de référence dont le potentiel est stable et ne dépend pas de la nature de la solution [7]. On mesure en fait la différence de potentiel qui se forme entre ces deux électrodes et non l’ORP. Dans l'écrasante majorité de cas, on utilise comme électrode de référence une électrode Ag/AgCl, argent/chlorure d'argent dont le potentiel est +200 millivolts (+0,2 Volt) par rapport à l'électrode normale d'hydrogène (0 Volt par définition). L'électrode de platine prend donc le potentiel ORP de la solution, mais l'instrument de mesure affiche la différence de potentiel entre l'ORP et le potentiel de l'électrode de référence. Il est donc tout à fait incorrect d'appeler ORP le potentiel affiché par le millivoltmètre.
[7]
Les électrodes modernes pour mesurer l'ORP sont des électrodes dites « combinées » dans lesquelles, à côté de l'électrode de platine, se trouve aussi une électrode de référence de Ag/AgCl. L'électrode commerciale ORP est en fait une pile composée d'une électrode de platine et d'une électrode de référence argent-chlorure d'argent. L'électrolyte de cette pile est la solution dont on se propose de mesurer l'ORP. On ne mesure donc pas un « potentiel », mais la force électromotrice d'une pile conventionnelle.
A titre de comparaison, le pH d'une solution est aussi mesuré à l'aide d'une électrode « combinée ». Ici aussi, on mesure la force électromotrice d'une pile composée d'une électrode d'argent/chlorure d'argent et d'une électrode de membrane de verre. Le potentiel de cette dernière est proportionnel au logarithme de l'activité protonique: pH =-log[H+].
Il n'y a donc pas de différence ni conceptuelle ni technique entre la mesure du pH et celle du rH2. Ces deux grandeurs se complètent et définissent d'une manière précise l'état de protonisation et d'électronisation d'une solution aqueuse. En ignorant le rH2, la détermination de l'état d'oxydation d'une solution devient problématique, voire impossible, du moins d'une manière précise.
La signification profonde de la notion du rH2
Qu’est-ce que « l’activité électronique »?
Tout le monde admet que le pH exprime le niveau d'échanges protoniques dans une solution aqueuse. Par contre, faute de connaître la notion du rH2, les scientifiques admettent d'une manière incorrecte que les propriétés oxydantes ou réductrices d'une solution ne sont caractérisées que par l'ORP. Nous allons à présent montrer que ceci n'est vrai que dans des conditions tout à fait particulières. Dans la majorité des cas, on est dans l'erreur.
Aux paragraphes consacrés à l'autoprotolyse et à l'autoélectrolyse de l'eau, nous avons vu que seule l'activité d'hydrogène [H2] peut caractériser l'état d'oxydation ou de réduction d'une solution par rapport à l'état de référence: l'eau chimiquement pure. L’activité d’hydrogène [H2] n'est en fait que l'activité électronique de la solution, puisque H2 se forme par le transfert de deux électrons e- sur deux protons H+ de l'eau pour former H2. Donc l'activité [H2] exprime l'état d'électronisation de la solution. Mais on peut alors poser la question de savoir ce que l'ORP mesuré signifie réellement. Nous arrivons ainsi à la deuxième ambiguïté de l'ORP.
La deuxième ambiguïté de l'ORP
La loi classique de Nernst (équation 11) définit le potentiel rédox E d'une manière explicite en le liant aux activités de la forme oxydée [Ox] et réduite [Red] d'un système (couple) redox donné. Chaque système redox est caractérisé par une demi-réaction de réduction:
Réducteur La forme oxydée d'un système capte donc n électrons pour se transformer en sa forme réduite. Par convention, les chimistes écrivent ce processus à l'aide d'une équation:
Red A titre d'exemple, le système chlorure/chlore ou Cl-/Cl2 est caractérisé par la demi-réaction de réduction: Cl2 + 2 e- 2 Cl-. L'oxydant chlore Cl2 capte donc deux électrons e- et, ce faisant, se réduit en ions chlorures Cl-. De même, l'ion de sodium Na+ (qui n'est autre que la forme oxydée du sodium métallique Na) peut aussi capter un électron pour se réduire en sodium métallique Na, suivant la réaction Na+ + e- → Na.
Un fait capital est que l'eau, en tant que solvant actif, se comporte comme un acide vis-à-vis d'une base et comme une base vis-à-vis d'un acide. C'est ce qu'on appelle le caractère amphotère (ou ampholyte) de l'eau. Il en va de même avec les oxydants et les réducteurs: en présence d'un réducteur, l'eau se comporte en oxydant (elle capte ses électrons), tandis qu'en présence d'un oxydant, elle se comporte en réducteur en lui donnant des électrons.
L'eau est donc elle-même un système redox capable de donner ou de capter des électrons des substances qu'on y dissout. Le système redox de l'eau est le système d'hydrogène/proton : H2/H+, caractérisé par la demi-réaction de réduction (l'échelle des potentiels ORP est précisément liée à cette réaction):
H2La forme oxydée de ce système est le proton H+ (ou plus exactement sa forme hydrolysée, l'ion hydroxonium H3O+), tandis que la forme réduite est l'hydrogène moléculaire H2. C'est d'ailleurs ce système qui fait fonctionner l'électrode d'hydrogène. En ce sens, toute solution aqueuse, quelle que soit sa composition chimique, peut être assimilée à l'électrolyte d'une électrode d'hydrogène (c'est d'ailleurs le premier postulat de la bioélectronique). Le potentiel que prendra dans cette solution une électrode métallique inerte (du platine, de l'or, du titane ou autre) ne dépendra in fine que de l'activité protonique [H+] et de l'activité électronique [H2] qui s'établit dans l'eau sous l'action des substances dissoutes (solutés). Donc quelle que soit la composition de la solution, l'électrode de platine ne détectera que ces deux activités. D'après la loi classique de Nernst, on peut donc écrire que le potentiel E (exprimé en Volt, et qui est en fait l’ORP réel) d'une telle électrode est:
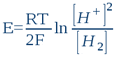
...où R = 8,316 Joule/mole.K (la constante des gaz parfaits); T est la température absolue exprimée en degrés Kelvin (25°C = 298K); et F = 96500 Coulombs/mole (la constante de Faraday ou la charge électrique d'une mole d'électrons). En passant aux logarithmes décimaux (lnx = 2,303logx) et en tenant compte de la définition du pH et du rH2, nous avons:
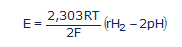
(#eq13)
L'équation (13) obtenue est d'une importance capitale, car elle montre la seconde ambiguïté de l'ORP [8]. Le potentiel redox E (qu'on appelle aussi ORP) est la somme algébrique de deux termes: le premier terme du côté droit de l'équation (13), ne dépend que des échanges électroniques rH2, le second uniquement des échanges protoniques pH. Ce qu'on mesure donc dans une solution avec un millivoltmètre dépend à la fois du pH et du rH2. Pour se prononcer sur le caractère oxydant ou réducteur (antioxydant) d'une solution, uniquement sur base d'une mesure d’ORP, sans tenir compte du pH de la solution, aboutit à des erreurs d'appréciation dans l'écrasante majorité des cas.
[8]
Connaissant donc la signification physique de l'équation (13), affirmer – ce que d'éminents collègues ont fait – que, « le rH2 n'existe pas, car c'est la combinaison linéaire arbitraire de deux mesures expérimentales, celle du potentiel E (ou ORP) et du pH » est pour le moins étrange. C'est d'autant plus étrange que les mesures expérimentales du rH2 et du pH se ramènent toutes les deux à une mesure de la force électromotrice d'une pile. En suivant cette logique, on pourrait aussi affirmer que le pH n'existe pas, car il est la combinaison linéaire de deux autres mesures expérimentales: l’ORP et le rH2.
La formule pratique pour calculer le rH2
(#correction_orp)
Compte tenu du fait, qu'à une température de 25°C = 298K, la valeur numérique du terme 2F/2,303RT = 33,8, à partir de l'équation (13) il est facile d'expliciter le rH2:
Dans cette équation, E n'est autre que le ORP (corrigé) exprimé en Volt.
Rappel important: Pour appliquer correctement l'équation (14), il faut tenir compte du fait que l'ORP réél n'est pas la valeur indiquée par le millivoltmètre relié à une électrode ORP (électrode de platine)! Au risque de se répéter, l'instrument ne mesure pas l'ORP, mais la différence de potentiel entre une électrode de platine plongée dans la solution et l'électrode de référence argent/chlorure d'argent dont le potentiel, par rapport à l'électrode normale d'hydrogène, est +200 millivolts à 25°C. Donc, pour obtenir la valeur correcte de l'ORP, (désigné E dans la formule 14) aux valeurs lues sur l'instrument, il faut ajouter 200 mV. Attention, dans les calculs E doit toujours être exprimé en Volt (1 Volt = 1000 mV).
A titre d'exemple, calculons le rH2 de l'eau minérale « Dasani » dont le pH est 3,04 et le potentiel mesuré par le millivoltmètre est +290 mV. La valeur de l'ORP ou E s'obtient en ajoutant à +290 mV les 200 mV du potentiel de l'électrode de référence Ag/AgCl: donc E=290+200=490mV = 0,49 Volt; pH = 3,04. Introduisons ces valeurs dans l'équation (14), pour obtenir:
En dépit de son caractère franchement acide, cette eau possède naturellement un caractère réducteur, ou antioxydant.
Prenons maintenant le cas d'une eau franchement basique, l'eau Essentia » avec un pH = 9,26 et un ORP mesuré de +179 mV = 0,179 Volt. Son rH2 = 33,8 x (0,179 + 0,200) + 2 x 9,26 = 31,3. En dépit de son caractère basique et de son ORP moins élevé que celui de l'eau Dasani, cette eau est oxydante.
En basant son jugement uniquement sur des valeurs affichées par le millivoltmètre, on aurait dit que « l'eau Dasani (+290 mV) est plus oxydante que l'eau Essentia (+179mV) » alors que c'est l'inverse qui est vrai.
La quantification W de Vincent
En bioélectronique médicale, on a souvent recours à une notion établie par Louis-Claude Vincent en 1973. A partir des coordonnées bioélectroniques, ce dernier a mis au point une méthode de calcul pour évaluer le « niveau d’énergie stockée dans l’organisme » et celle qui est « éliminée ». A cette fin, il a appliqué les lois de l’électricité classique au potentiel redox ORP (que nous désignons dans les calculs par E) et à la résistivité ρ (prononcer « rô ») du milieu aqueux.
Il s'agit d'une notion empirique dont même Vincent n'a pas jugé utile de donner la signification physique précise. En 1992, nous avons tenté d'établir un modèle thermodynamique pour cette notion. [Réf.: Országh J. « Quelques aspects physico-chimiques des coordonnées bioélectroniques », Réf.: Sciences du Vivant (Éd. Arys, Paris), volume 4, pages 45-62 (1992)].
Tout système redox peut être schématisé à l’aide d’une pile constituée d’une électrode normale d’hydrogène et d’une électrode contenant en solution le système redox étudié. La force électromotrice (ou l’enthalpie libre à une constante près) de cette pile est évidemment égale à E. Nous pouvons poser par convention [9] (comme Vincent l’a fait implicitement) qu’une électrode inerte de s = 1 cm2 de surface est plongée dans une proportion de 1 cm3 de cet électrolyte dont la résistivité est ρ. La puissance maximale W de cette pile sera donc:
(#eq15)
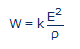
...où k est une constante dont la valeur numérique vaut 1 cm2/cm. Si E est exprimé en millivolts et ρ en ohm.cm, on obtient W en microwatts (µW). En fait, cette constante est le rapport de surface s de l’électrode et la distance ℓ parcourue par le courant à travers la pile: k=s/ℓ. Le terme W exprime la vitesse maximale de production d'énergie électrique par cette pile hypothétique et conventionnelle.
[9]
Bien que non explicitée dans les travaux de Vincent, cette convention y est présente implicitement. Si la constante k était différente de 1, les formules de Vincent ne donneraient pas les valeurs calculées par leur auteur. En fait, Vincent n'a jamais indiqué k dans ses formules qui, de ce fait, sont incohérentes au point de vue dimensionnel. C'est pour lever cette incohérence que nous avons tenu à introduire k et lui donner une signification physique.
Remplaçons la valeur de E tirée de l'équation (14), dans l'équation (15), en tenant compte du fait que k=1cm2/cm:
(#eq16) La valeur de 8,75.10-4 n'est valable qu'à 25°C. À une température T différente il faut remplacer la constante 33,8 par 2F/2,303RT. Dans la pratique, les instruments de mesure affichent non pas la résistivité ρ, mais sa valeur réciproque, la conductivité κ (prononcer « kappa »): κ=1/ρ. Si la conductivité est exprimée en µS/cm (prononcer « microSiemens par cm »), la formule pratique pour calculer W est: Dans ce cas, on obtient la quantification de Vincent W, en µW (prononcer « microwatt »). A titre d'exemple, calculons la quantification de Vincent W d'une eau de distribution dont la conductivité est κ = 650 µS/cm, dont le rH2 = 30,5 et le pH = 7,6: En comparaison, une eau biocompatible obtenue par microfiltration au départ de l'eau de pluie aura une conductivité κ = 35 µS/cm, rH2 = 28,5 et pH= 7,2: Les valeurs guide pour une eau biocompatible sont données dans un tableau.
