Unitary Theory of Redox and Acid-base Reactions – the Meaning of ORP

Electrical charge exchanges in water

If water and the aqueous medium are considered a « miracle of nature », it is in thanks to their remarkable properties related to the exchange of positive electric charges or H⁺ protons and negative electric charges or e^– electrons. The former are the acid-base reactions, the second those of oxidation-reduction. In all the treaties of chemistry, both types of reactions are treated in separate chapters. And yet, with regard to simple transfer of electric charges, these two types of reactions can be described by a single mathematical formalism, the unitary theory of charge transfer reactions in aqueous media. As we will show, this theory clearly shows the intimate connection of these two types of reactions. The considerations herein are obviously only valid in an aqueous medium [1].

Auto-protolysis of water

Between two water molecules, there may be spontaneous proton transfer, a positive electric charge (the proton is the nucleus of a hydrogen atom, designated by H⁺), through a reaction called « auto-protolysis »:

H₂O + H₂O H₃O⁺ + OH^–

To simplify, chemists often adopt a convention which replaces the writing of the hydroxonium ion H₃O⁺ (in fact the hydrolysed proton, not to be confused with the « hydranion » ion H₃O^–) by the proton H⁺, knowing of course that this is only a writing convention. In reality, a proton can never « travel » alone in water without being bonded to a molecule of H₂O, no more so than hydranion. Therefore, reaction (1) simply reads:

H₂O H⁺ + OH^–

The OH^– ion is called hydroxide. The equilibrium constant K_w of the auto-protolysis reaction (1a) reads:

...where [H⁺] and [OH^–] are the activities of those protons and hydroxide ions. As a first approximation [H⁺] and [OH^–] can often be treated as molar concentrations expressed in moles/litre. In electrochemistry and thermodynamics, it is more correct to speak of activity instead of concentration. Activity is a dimensionless number.

Once dissolved in water, acids release protons thereby increasing the activity of H⁺ ions (which we shall now read as [H⁺]), called proton activity. On the other hand, the bases are likely to release hydroxide ions OH^– by increasing their activity [OH^–]. However, by means of Equation (2) in an aqueous medium, a balance is always established between these two ions, so that the product of their activities remains constant at a value of 10^–14. Thus, there is a certain « balance » between the two: when proton activity increases, hydroxide ion activity decreases, and vice versa.

To characterize the acidity or alkalinity of an aqueous solution, Sørensen, a Danish doctor and biochemist introduced in 1909 the concept of « hydrogen potential », which he expressed as « pH₂ » [2]., which later became « pH » that we now define as: pH = – log[H⁺]. This also calls for the complementary concept of pOH, defined in a similar manner: pOH = –log[OH^–]. Similarly, the auto-protolysis constant can also be expressed in the same logarithmic form: pK_w = –logK_w = –log10^–14 = 14. Therefore, Equation (2) can be written in a logarithmic form:

Obviously, the reference state for aqueous solutions is chemically pure water in which the acidity and alkalinity are balanced: the medium is neutral. In this case, the activities of protons and hydroxide ions are the same: [H⁺] = [OH^–] = 10^–7. In a solution where this condition is fulfilled, the result is pH= – log10^–7 = 7. This is the point of acid-base neutrality. Solutions with a pH between 0 and 7 are called « acid », those whose pH is between 7 and 14 are called « basic » (or « alkaline ») [3].

[2]
Unwittingly, Sørensen’s pH₂ prefigured the notion of rH₂ launched in 1920 by the American physical chemist WM Clark. In fact the two variables are closely linked to the H₂ hydrogen molecule. Upon contact with water, this molecule undergoes a bona fide electrolytic dissociation: H₂ + 2H₂O H₃O⁺ + H₃O^- detected by measuring the potential of the solution in which is sparged hydrogen gas. Sørensen’s pH is none other than -log[H₃O⁺], while Clark’s rH₂ is -log[H₃O^-]. The parallel between the two concepts is more than obvious. Furthermore, neither Sørensen nor Clark were electrochemists. Only, Sørensen was luckier to have friends among the electrochemists of his time unlike Clark who was subjected to a genuine scientific inquisition by the American Chemical Society, for his rH₂ concept. In 1924 he was forced to make a public self-criticism and withdraw his invention. Because of this, the science of electrochemistry was deprived of an essential tool, the consequences of which are becoming extremely annoying as they are an obstacle to the development of promising applications in electrochemistry and thermodynamics, particularly in medicine.

Auto-electrolysis of water

The concepts outlined in the preceding paragraph are, in principle, known to high school students. Those that follow are far less known to the public, even by specialists.

In the fields of electrochemistry and thermodynamics of aqueous solutions, the reference state is chemically pure water. The standard reaction of formation of water

H₂ + ½ O₂ H₂O

...is the basis for calculating the thermodynamic functions of the water molecule starting from electrochemical and calorimetric data. The reverse of this reaction is what we call « auto-electrolysis » of water that takes place when 4 (negatively charged) electrons e- are exchanged between two water molecules, giving rise to two hydrogen molecules and one oxygen molecule:

H₂O + H₂O 2 H₂ + O₂

Reminder: auto-protolysis takes place by (positively charged) proton exchanges between two water molecules. The parallelism between auto-protolysis and auto-electrolysis is obvious. Also see the table in the next chapter. The equilibrium constant K_e for reaction (5) thus reads:

In fact, the water molecule’s oxygen yields two electrons to the two hydrogen atoms. These two atoms combine to make a di-hydrogen molecule H₂. The oxygen having lost two electrons « seeks » another, in the same situation, to form the di-oxygen molecule O₂ [4]. The water's auto-electrolysis constant K_e can be calculated from the standard Gibbs energy (i.e. free enthalpy) of water formation.

When dissolving a reducing agent in water, it will tend to yield electrons to the water. On the other hand, the oxidizing agent will capture electrons. The presence of a reducing agent will move the auto-electrolytic balance towards the formation of hydrogen H₂, while the oxidizing agent will foster the appearance of oxygen O₂. Here, too, thanks to the the equilibrium (5), there is balance between hydrogen [H₂] and oxygen [O₂] activities. Both interchange, as in the case of [H⁺] et [OH^–].

Definition of rH₂

In 1920, seven years after the pH concept was introduced to the world, W.M. Clark defined a similarly-structured notion [5], the concept of rH₂:

In parallel, we can also define the rO₂ = –log[O₂]. Thenceforth, considering Equation (6), Equation (3) for redox reactions will read:

« Redox neutrality » or the concept of « redox indifference »

For redox reactions, the reference medium is also chemically pure water, in which hydrogen [H₂] and oxygen [O₂] activities are divided in proportions of one oxygen for two hydrogen: [H₂] = 2 [O₂]. Let’s therefore calculate the rH₂ of chemically pure water. To do so, in Equation (6), replace [O₂] by ½[H₂]

...from which one obtains the activity of hydrogen in pure water: [H₂] = 10^–27.7 that chemists round to 10^–28. Pure water’s rH₂ is therefore –log10^–28 = 28. This is called the point of « redox neutrality » or « redox indifference ».

So regardless of the pH value, an aqueous solution is neither oxidative nor reductive (or anti-oxidative) when its rH₂ is equal to 28. A solution whose rH₂ is located between 0 and 28 is called reductive and antioxidant. When the value of rH₂ is between 28 and 42, the solution is called oxidant [6].

Stability limits of aqueous solutions

A solution in which the activity of oxygen [O₂] = 1, rO₂ being zero under Equation (8), rH₂=42. This is the upper limit of thermodynamic stability of an aqueous solution. At this value, gaseous oxygen O₂ is released, but especially, highly reactive atomic oxygen O is formed: what used to be called « nascent oxygen ».

A solution in which rH₂ is zero has an activity of hydrogen [H₂] = 1. It is the lower limit of thermodynamic stability of an aqueous solution. At this value, water decomposes and releases « nascent hydrogen » H, electrically neutral. This hydrogen has a high affinity to free radicals, which are also carriers of an unpaired electron.

A negative value for the rH₂ has in principle no physical meaning. However, negative values have been measured under particular conditions. Here we enter the realm of reversible processes in the field of thermodynamics. We are looking at aqueous solutions that are unstable from a thermodynamic perspective, in which nascent hydrogen is temporarily stabilised in a different molecular formation: hydranion H₃O^–. This is probably the case of hydrogen water.

ORP’s first ambiguity

Potential redox ORP is an experimental measure (in volts or millivolts) widely used to characterize the redox properties of aqueous solutions. It is generally accepted that the greater the ORP, the more oxidative the solution; the lower the ORP, the more the solution is reductive or « anti-oxidative ». This assertion is only true at pH = constant.

The ORP readings on a measuring instrument have two ambiguities:

• It’s not the actual ORP used in electrochemical and thermodynamic calculations. For this, the reading must be corrected.
  
• Even the real (i.e. corrected) ORP is only one of the elements needed ascertain the oxidative or antioxidative character of an aqueous solution.

Now let's look at the first ambiguity.

Conventional scale of ORP potentials

Now consider the nature of ORP from an electrochemical point of view. The ORP scale’s true zero point does not correspond to the zero potential reading observed on a voltmeter. The latter in no way represents a solution’s redox point of indifference (or neutrality), i.e. above which the solution is oxidative, and below which it is reductive. In fact, the zero potential stems from the concept of thermodynamic stability limits in aqueous solutions. This condition is achieved at the standard hydrogen electrode, more specifically a platinum electrode coated with a metallic platinum sponge (also called a « platinized » platinum electrode), dipped in a solution having a pH=0, in which hydrogen gas H₂ is sparged at a pressure of one bar.

The hydrogen adsorbed in the pores of the platinum sponge behaves as an element in a condensed state, in which the thermodynamic activity is equal to: [H₂] = 1. So the electrolyte in contact with the platinum electrode has an rH₂ of zero. At pH = rH₂ = 0, on the platinum electrode, we measure a remarkably stable potential with a value is zero {under the Nernst Law: Equation (11)} [7]. The thermodynamic zero potential therefore has a precise physical meaning; its value is linked to the simultaneous cancellation of pH and rH₂.

To dispel misunderstandings leading to errors, remember that the zero potential reading on an ORP measuring instrument does not equate to the thermodynamic ORP and in no way corresponds to the redox indifference point above which there is an oxidative milieu, and below which there is a reductive or (antioxidant) milieu.

Measuring the ORP

To measure a solution’s ORP, two electrodes are plunged into it: a platinum electrode (inert vs water) and a reference electrode with a stable potential (inert vs the solution) [8]. The resulting difference in potential between the two electrodes is thence measured, not the ORP. In the overwhelming majority of cases, the reference electrode is a silver chloride electrode (Ag/AgCl) whose potential is +200 millivolts (+0.2 volts) with respect to the standard hydrogen electrode (which is 0 Volt by definition). The platinum electrode thus takes the solution’s potential ORP, but the voltmeter displays the difference in potential between the ORP and the reference electrode’s potential. It is therefore quite inappropriate to designate the potential displayed by the voltmeter as being the « ORP ».

Underlying significance of the rH₂ concept

What is « electron activity »?

Everyone agrees that pH expresses the proton exchange level in an aqueous solution. However, without an understanding of rH₂, scientists incorrectly consider that the oxidative or reductive properties of a solution are characterized only by the ORP. We will now show that this is true only under special circumstances(only at pH = constant). In most cases, the assumption is wrong.

The paragraphs on water’s auto-protolysis and auto-electrolysis have shown that only hydrogen [H₂] activity can characterize a solution’s oxidative or reductive state with respect to the reference state (i.e. chemically pure water). Hydrogen [H₂] activity is in fact the solution’s electron activity, since H₂ is formed by the transfer of two electrons e^– on two water protons H⁺. Thus the activity [H₂] expresses the solution’s state of electronicization. But we can then ask what the measured ORP really means. This brings us to ORP’s second ambiguity.

ORP’s second ambiguity

The classical Nernst equation (equation 11) explicitly defines the ORP by relating it to activities of the oxidized [Ox] and reduced [Red] forms of a given redox (couple) system. Each system is characterized by a redox reductive half-reaction: Oxidative + n electrons Reductive. A system’s oxidized form thus captures n electrons to transform into its reduced form. By convention, chemists write this process using an equation:

Oxidant + n electrons Reductant

The oxidized form of a system thus captures n electrons to turn into its reduced form. By convention, chemists write the process using the following equation:

Ox + n e^– Red

For example, the chloride/chlorine system or Cl^–/Cl₂ is characterized by the half-reduction reaction: Cl₂ + 2 e^– 2 Cl^–. Oxidative chlorine Cl₂ thus captures two electrons e^–, and is thereby reduced into chloride ions Cl^–. Similarly, the sodium ion Na⁺ (which is simply the oxidized form of metallic sodium Na) can also capture an electron to be reduced into metallic sodium Na, as per the reaction Na⁺ + e^– → Na.

A major fact is that water, as an active solvent, has an amphoteric (or amphiprotic) character, i.e. it behaves as an acid vis-à-vis a base, and as a basis vis-à-vis an acid. The same goes for oxidants and reductants: in the presence of a reducing agent, water behaves as an oxidant (it captures electrons), whereas in the presence of an oxidant, it acts as a reductant by yielding electrons.

So water is itself a redox system that can give or capture electrons from the substances that are dissolved into it. Water’s redox system is the hydrogen/proton system: H₂/H⁺, characterized by the half-reduction reaction (n.b. the ORP scale is specifically related to this reaction):

This system’s oxidized form is the proton H⁺ (or more exactly its hydrolysed form – hydroxonium ion H₃O⁺), while the reduced form is molecular hydrogen H₂. Indeed, this system is what makes the hydrogen electrode work. In this sense, any aqueous solution, whatever its chemical composition, can be likened to a hydrogen electrode’s electrolyte (n.b. this is indeed the first postulate of bioelectronics). The potential to be acquired in this solution by an inert metal electrode (e.g. platinum, gold, titanium or otherwise) will ultimately depend on the proton [H⁺] and electron [H₂] activities that settles in the water by the action of dissolved substances (i.e. solutes). So whatever the solution’s composition, the platinum electrode will only detect these two activities. According to the classic Nernst equation, we can write that such an electrode’s potential E (in volts, constituting the true ORP) is:

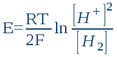
...where R = 8.316 Joule/mole.K (the gas constant), T is absolute temperature in degrees Kelvin (25°C = 298K) and F = 96500 Coulombs/mol (i.e. Faraday's constant or the electric charge a one mole of electrons). By shifting to decimal logarithms (lnx = 2,303logx) and taking into account the definition of pH and rH₂, we have:

...or else

The resulting Equation (13) is of paramount importance because it shows ORP’s second ambiguity [9]. The redox potential E (also known as ORP) is the algebraic sum of two terms: the first term on the right side of Equation (13) depends only on the electron exchanges rH₂, the second only on proton exchanges pH. What we therefore measure in a solution using a voltmeter depends on both pH and rH₂. To rule on the oxidative or the reductive (i.e. antioxidative) character of a solution, solely based on an ORP measurement and regardless of the solution’s pH leads to miscalculations in the overwhelming majority of cases.

Practical formula for calculating rH₂

Given the fact that at a temperature of 25°C = 298K, the numerical value of the term 2F/2.303RT = 33.8, from Equation (13) it is easy to explain rH₂:

In this equation, E is the (corrected) ORP expressed in volts.

Important Note: To properly apply Equation (14), you must take into account that the true ORP is not the value indicated by the voltmeter connected to an ORP electrode (i.e. the platinum electrode)! We must insist: the instrument does not measure the ORP, but the difference in potential between a platinum electrode immersed in the solution and the reference silver chloride electrode whose potential, compared to the standard hydrogen electrode, is +200 mV at 25°C. So to get the correct ORP value (designated E in equation 14) with readings on the instrument, you must add 200 mV. Careful: in the calculations, E must always be expressed in Volts (n.b. 1 Volt = 1000 mV).

For example, calculate the rH₂ of « Dasani » water whose pH is 3.04 and the potential measured by the voltmeter is +290 mV. The value of the ORP (or E) is obtained by adding the Ag/AgCl reference electrode potential’s 200 mV to the measured value +290 mV: therefore E=290+200=490mV = 0.49 Volt; pH = 3.04. Introduce these values in Equation (14), to obtain:

Despite its clearly acidic character, this water naturally has a reductive character (i.e. antioxidative).

Now consider a clearly alkaline water, « Essentia » water having a pH = 9.26 and a measured ORP of +179 mV = 0.179 Volt. Its rH₂ = 33.8 x (0.179 + 0.200) + 2 x 9.26 = 31.3. This water, despite its alkaline nature and its lower ORP (compared to Dasani water) is in fact oxidative.

By basing one’s decision solely on the values displayed by the voltmeter, one would have said that « Dasani water (+290 mV) is more oxidative than Essentia water (+179 mV) », while the opposite is true.

Vincent’s Quantization Value (W)

In medical bioelectronics, we often use a concept established in 1973 by Louis-Claude Vincent. Starting from bioelectronic coordinates, Vincent developed a methodology for assessing the « level of energy stored in the body » and that energy which is « eliminated ». To this end, he applied the laws of conventional electricity to redox ORP (which we refer to in the calculations as E) and the aqueous medium’s resistivity ρ (pronounced as « rho »).

It’s an empirical notion that even Vincent did not see fit to give the precise physical meaning for. In 1992, we attempted to establish a thermodynamic model for this notion. [Ref.: Országh J., Some physicochemical aspects of bio-electronic coordinates, Sciences du Vivant (Éd. Arys, Paris), volume 4, pages 45-62 (1992)]

All redox systems can be diagrammed with a battery consisting of a standard hydrogen electrode and an electrode in solution containing the redox system studied. This battery’s electromotive force (or Gibbs to a constant) is obviously equal to E. By convention [10], (and as assumed implicitly by L.-C. Vincent), we can assume that an inert electrode having a surface area s = 1 cm² is immersed in a proportion of 1 cm³ of this electrolyte whose resistivity is ρ. The maximum power W of this battery will thus be

Now place the E value derived from Equation (14) into Equation (15), taking into account that k=1cm²/cm:

Guideline values for biocompatible water can be found in the table on this subject.

TOP